이진 분류
회귀와 같은 분류는 감독되는 기계 학습 기술입니다. 따라서 모델을 학습, 유효성 검사 및 평가하는 동일한 반복 프로세스를 따릅니다. 회귀 모델과 같은 숫자 값을 계산하는 대신 분류 모델을 학습시키는 데 사용되는 알고리즘은 클래스 할당에 대한 확률 값을 계산하고 모델 성능을 평가하는 데 사용되는 평가 메트릭은 예측 클래스를 실제 클래스와 비교합니다.
이진 분류 알고리즘은 단일 클래스에 대해 가능한 두 레이블 중 하나를 예측하는 모델을 학습시키는 데 사용됩니다. 기본적으로 true 또는 false를 예측합니다. 대부분의 실제 시나리오에서 모델 학습 및 유효성 검사에 사용되는 데이터 관찰은 여러 기능(x) 값과 1 또는 0인 y 값으로 구성됩니다.
예제 - 이진 분류
이진 분류의 작동 방식을 이해하려면 단일 기능(x)을 사용하여 레이블 y 가 1 또는 0인지 예측하는 간소화된 예제를 살펴보겠습니다. 이 예제에서는 환자의 혈당 수준을 사용하여 환자에게 당뇨병이 있는지 여부를 예측합니다. 모델을 학습시킬 데이터는 다음과 같습니다.

|

|
|---|---|
| 혈당 (x) | 당뇨병? (y) |
| 67 | 0 |
| 103 | 1 |
| 114 | 1 |
| 72 | 0 |
| 116 | 1 |
| 65 | 0 |
이진 분류 모델 학습
모델을 학습하기 위해 학습 데이터를 클래스 레이블이 true일 확률을 계산하는 함수에 맞추는 알고리즘을 사용합니다(즉, 환자에게 당뇨병이 있는 경우). 확률은 0.0에서 1.0 사이의 값으로 측정되므로 가능한 모든 클래스의 총 확률은 1.0입니다. 예를 들면, 당뇨병을 가진 환자의 확률이 0.7인 경우에, 그 때 환자가 당뇨병이 아니라 는 것을 0.3의 해당 확률이 있습니다.
다음과 같이 0.0에서 1.0 사이의 값을 가진 시그모이드(S자형) 함수를 파생시키는 로지스틱 회귀와 같이 이진 분류에 사용할 수 있는 많은 알고리즘이 있습니다.

비고
이름에도 불구하고 기계 학습 로지스틱 회귀 는 회귀가 아닌 분류에 사용됩니다. 중요한 점은 생성되는 함수의 로지스틱 특성으로, 이진 분류에 사용되는 경우 0.0과 1.0 사이의 S자형 곡선을 설명합니다.
알고리즘에 의해 생성된 함수는 지정된 x 값에 대해 y가 true(y=1)일 확률을 설명합니다. 수학적으로 다음과 같이 함수를 표현할 수 있습니다.
f(x) = P(y=1 | x)
학습 데이터에서 6개의 관찰 중 3개에 대해 y 가 확실히 사실임을 알고 있으므로 y=1이 1.0 이고 다른 세 가지 관찰의 경우 y 가 확실히 거짓이라는 것을 알고 있으므로 y=1의 확률은 0.0입니다. S자형 곡선은 선에서 x 값을 그리면 y 가 1인 해당 확률을 식별할 수 있도록 확률 분포를 설명합니다.
이 다이어그램에는 이 함수를 기반으로 하는 모델이 true(1) 또는 false(0)를 예측하는 임계값을 나타내는 가로선도 포함되어 있습니다. 임계값은 y (P(y) = 0.5)의 중간 지점에 있습니다. 이 시점 이상의 값에 대해 모델은 true (1)를 예측합니다. 이 지점 아래의 모든 값에 대해 false (0)를 예측합니다. 예를 들어, 혈당 수준이 90인 환자의 경우 이 함수는 확률 값이 0.9가 될 수 있습니다. 0.9는 0.5의 임계값보다 높기 때문에 모델은 true (1)를 예측합니다 - 즉, 환자는 당뇨병이 있을 것으로 예측됩니다.
이진 분류 모델 평가
회귀와 마찬가지로 이진 분류 모델을 학습할 때 학습된 모델의 유효성을 검사할 데이터의 임의의 하위 집합을 보류합니다. 당뇨병 분류자의 유효성을 검사하기 위해 다음 데이터를 보류한 것으로 가정해 보겠습니다.
| 혈당 (x) | 당뇨병? (y) |
|---|---|
| 66 | 0 |
| 107 | 1 |
| 응급 전화번호 112 | 1 |
| 71 | 0 |
| 87 | 1 |
| 89 | 1 |
이전에 파생된 로지스틱 함수를 x 값에 적용하면 다음 그림이 나타납니다.
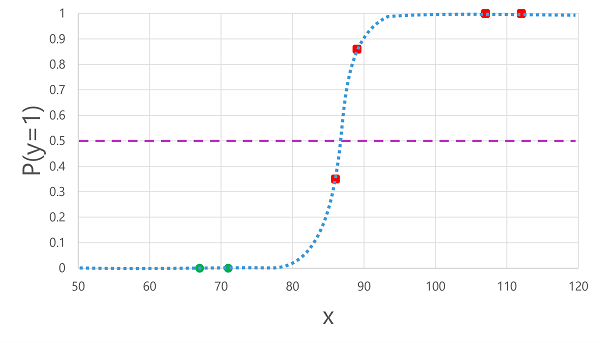
함수에 의해 계산된 확률이 임계값 이상인지 또는 그 미만인지에 따라 모델은 각 관찰에 대해 1 또는 0의 예측 레이블을 생성합니다. 그런 다음 예측 클래스 레이블 (ŷ)을 실제 클래스 레이블 (y)과, 다음과 같이 비교할 수 있습니다.
| 혈당 (x) | 실제 당뇨병 진단(y) | 예측된 당뇨병 진단 (ŷ) |
|---|---|---|
| 66 | 0 | 0 |
| 107 | 1 | 1 |
| 응급 전화번호 112 | 1 | 1 |
| 71 | 0 | 0 |
| 87 | 1 | 0 |
| 89 | 1 | 1 |
이진 분류 평가 메트릭
이진 분류 모델에 대한 평가 메트릭을 계산하는 첫 번째 단계는 일반적으로 가능한 각 클래스 레이블에 대한 정확하고 잘못된 예측 수의 행렬을 만드는 것입니다.

이 시각화를 혼동 행렬이라고 하며 다음 위치에서 예측 합계를 보여 줍니다.
- ŷ=0 및 y=0: 참 부정 (TN)
- ŷ=1 및 y=0: 가양성 (FP)
- ŷ=0 및 y=1: 가음성 (FN)
- ŷ=1 및 y=1: 참 긍정 (TP)
혼동 행렬의 정렬은 올바른(true) 예측이 왼쪽 위에서 오른쪽 아래의 대각선으로 표시되도록 합니다. 종종 색 강도는 각 셀의 예측 수를 나타내는 데 사용되므로 잘 예측하는 모델을 한눈에 보면 깊이 음영 처리된 대각선 추세가 표시됩니다.
정확도
혼동 행렬에서 계산할 수 있는 가장 간단한 메트릭은 정확도 입니다. 모델이 올바르게 얻은 예측의 비율입니다. 정확도는 다음과 같이 계산됩니다.
(TN+TP) ÷(TN+FN+FP+TP)
당뇨병 예제의 경우 계산은 다음과 같습니다.
(2+3) ÷(2+1+0+3)
= 5 ÷ 6
= 0.83
따라서 유효성 검사 데이터의 경우 당뇨병 분류 모델은 83% 정확한 예측을 생성했습니다.
정확도는 처음에는 모델을 평가하는 데 좋은 메트릭처럼 보일 수 있지만 이를 고려합니다. 인구의 11% 당뇨병이 있다고 가정해 봅시다. 항상 0을 예측하는 모델을 만들 수 있으며, 특징을 평가하여 환자를 구분하려고 실제로 시도하지 않더라도 89%정확도를 달성할 수 있습니다. 우리가 진정으로 필요로하는 것은 모델이 긍정적 인 경우 1 을 예측하고 부정적인 경우 0 을 예측하는 방법을 더 깊이 이해하는 것입니다.
리콜
재현율은 모델이 올바르게 식별한 긍정 사례의 비율을 측정하는 메트릭입니다. 다른 말로 , 당뇨병이 있는 환자의 수에 비교된, 얼마나 많은 모형이 당뇨병이 있을 것으로 예측 했습니까?
리콜 공식은 다음과 같습니다.
TP ÷(TP+FN)
당뇨병 예제:
3 ÷(3+1)
= 3 ÷ 4
= 0.75
그래서 우리의 모형은 당뇨병이 있는 환자의 75%를 정확하게 식별했습니다.
정밀성
정밀도 는 재현율과 유사한 메트릭이지만 실제 레이블이 실제로 양수인 예측 긍정 사례의 비율을 측정합니다. 즉, 모델에 의해 당뇨병이 있다고 예측된 환자 중 실제로 당뇨병이 있는 환자의 비율은 얼마인가요?
정밀도의 수식은 다음과 같습니다.
TP ÷(TP+FP)
당뇨병 예제:
3 ÷(3+0)
= 3 ÷ 3
= 1.0
그래서 우리 모형에 의해 당뇨병이 있을 것으로 예측된 환자의 100%가 실제로 당뇨병을 가지고 있습니다.
F1 점수
F1 점수 는 재현율과 정밀도를 결합한 전체 메트릭입니다. F1 점수의 수식은 다음과 같습니다.
(2 x 정밀도 x 재현율) ÷ (정밀도 + 재현율)
당뇨병 예제:
(2 x 1.0 x 0.75) ÷(1.0 + 0.75)
= 1.5 ÷ 1.75
= 0.86
곡선 아래 영역(AUC)
회수의 또 다른 이름은 TPR(참 긍정 비율)이며 FP÷(FP+TN)로 계산되는 FPR(가양성 비율)이라는 동일한 메트릭이 있습니다. 임계값 0.5를 사용할 때 모델의 TPR이 0.75임을 이미 알고 있으며 FPR에 대한 수식을 사용하여 0÷2 = 0 값을 계산할 수 있습니다.
물론 모델이 true (1)를 예측하는 임계값을 변경하려는 경우 양수 및 음수 예측 수에 영향을 줍니다. 따라서 TPR 및 FPR 메트릭을 변경합니다. 이러한 메트릭은 0.0에서 1.0 사이의 가능한 모든 임계값에 대해 TPR 및 FPR을 비교하는 수신된 ROC( 연산자 특성 ) 곡선을 그려 모델을 평가하는 데 자주 사용됩니다.

완벽한 모델에 대한 ROC 곡선은 왼쪽의 TPR 축을 똑바로 위로 이동한 다음 위쪽의 FPR 축을 가로 질러 이동합니다. 곡선의 플롯 영역이 1x1을 측정하므로 이 완벽한 곡선 아래의 영역은 1.0이 됩니다(모델이 올바른 100%임). 반면, 왼쪽 아래에서 오른쪽 위까지의 대각선은 이진 레이블을 임의로 추측하여 달성할 결과를 나타내며, 0.5의 곡선 아래 영역을 생성합니다. 즉, 두 개의 가능한 클래스 레이블을 감안할 때 50% 시간을 정확하게 추측할 것으로 예상할 수 있습니다.
당뇨병 모델의 경우 위의 곡선이 생성되고 AUC(곡선) 메트릭 아래의 영역 은 0.875입니다. AUC가 0.5보다 높기 때문에, 우리는 환자가 무작위로 추측하는 것보다 당뇨병이 있는지 여부를 예측하는 데 모델이 더 나은 성능을 발휘하는 것으로 결론을 내릴 수 있습니다.